Mathematics teacher educators’ noticing of pedagogical content knowledge on hierarchical classification of quadrilateral
##plugins.themes.bootstrap3.article.main##
Abstract
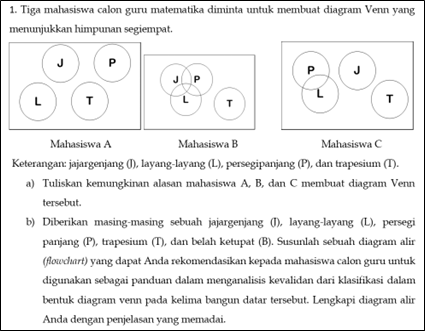
This study aims to investigate mathematics teacher educators’ (MTE) knowledge in noticing preservice teachers’ pedagogical content knowledge (PCK) on the hierarchical classification of the quadrilateral. A multiple case study was conducted to analyze the responses of ten MTEs in an online moderated-forum group discussion (M-FGD) from their written work on the MTE-PCK test completed prior to the M-FGD. The PCK test consisted of two tasks: the task that examines MTEs’ knowledge to predict pre-service teachers’ reason in representing the hierarchical classification of quadrilateral in Venn diagrams, and the task that examines MTEs’ knowledge in making a flowchart as a recommendation to mathematics teacher to analyze the validity of quadrilateral classification. Results show that the MTEs indicate two considerations of noticing pre-service teachers’ PCK on the quadrilateral classification: by definition and properties of quadrilaterals and by the visual appearance of quadrilaterals. Despite this, 20% of them were indicated to perform a lack of understanding of the hierarchical classification of quadrilaterals, as indicated by invalid flowcharts of validating the hierarchical classification of the quadrilateral.
##plugins.themes.bootstrap3.article.details##

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
The author is responsible for acquiring the permission(s) to reproduce any copyrighted figures, tables, data, or text that are being used in the submitted paper. Authors should note that text quotations of more than 250 words from a published or copyrighted work will require grant of permission from the original publisher to reprint. The written permission letter(s) must be submitted together with the manuscript.References
Amador, J. M., Bragelman, J., & Superfine, A. C. (2021). Prospective teachers’ noticing: A literature review of methodological approaches to support and analyze noticing. Teaching and Teacher Education, 99, 103256. https://doi.org/10.1016/j.tate.2020.103256
Avcu, R. (2022). Pre-service middle school mathematics teachers’ personal concept definitions of special quadrilaterals. Mathematics Education Research Journal, 1-46. https://doi.org/10.1007/s13394-022-00412-2
Beswick, K., & Goos, M. (2018). Mathematics teacher educator knowledge: What do we know and where to from here? Journal of Mathematics Teacher Education, 21(5), 417-427. https://doi.org/10.1007/s10857-018-9416-4
Birgin, O., & Özkan, K. (2022). Comparing the concept images and hierarchical classification skills of students at different educational levels regarding parallelograms: a cross-sectional study. International Journal of Mathematical Education in Science and Technology, 1-33. https://doi.org/10.1080/0020739X.2022.2052196
Chick, H., Baker, M., Pham, T., & Cheng, H. (2006). Aspects of teachers’ pedagogical content knowledge for decimals Proceedings of the 30th annual conference of the International Group for the Psychology of Mathematics Education,
Chick, H., & Beswick, K. (2018). Teaching teachers to teach Boris: A framework for mathematics teacher educator pedagogical content knowledge. Journal of Mathematics Teacher Education, 21(5), 475-499. https://doi.org/10.1007/s10857-016-9362-y
Craine, T. V., & Rubenstein, R. N. (1993). A quadrilateral hierarchy to facilitate learning in geometry. The Mathematics Teacher, 86(1), 30-36. https://doi.org/10.5951/mt.86.1.0030
de Villiers, M. (1994). The role and function of a hierarchical classification of quadrilaterals. For the learning of Mathematics, 14(1), 11-18.
Ekawati, R., Lin, F.-L., & Yang, K.-L. (2015). Primary teachers’ knowledge for teaching ratio and proportion in mathematics: The case of Indonesia. Eurasia Journal of Mathematics, Science and Technology Education, 11(3), 513-533. https://doi.org/10.12973/eurasia.2015.1354a
Erdogan, E. O., & Dur, Z. (2014). Preservice mathematics teachers’ personal figural concepts and classifications about quadrilaterals. Australian Journal of Teacher Education (Online), 39(6), 107-133. https://search.informit.org/doi/10.3316/ielapa.479231204395511
Erez, M. M., & Yerushalmy, M. (2006). “If you can turn a rectangle into a square, you can turn a square into a rectangle ...” Young students experience the dragging tool. International Journal of Computers for Mathematical Learning, 11(3), 271-299. https://doi.org/10.1007/s10758-006-9106-7
Forsythe, S. K. (2015). Dragging maintaining symmetry: can it generate the concept of inclusivity as well as a family of shapes? Research in Mathematics Education, 17(3), 198-219. https://doi.org/10.1080/14794802.2015.1065757
Fujita, T. (2012). Learners’ level of understanding of the inclusion relations of quadrilaterals and prototype phenomenon. The Journal of Mathematical Behavior, 31(1), 60-72. https://doi.org/10.1016/j.jmathb.2011.08.003
Fujita, T., & Jones, K. (2007). Learners’ understanding of the definitions and hierarchical classification of quadrilaterals: Towards a theoretical framing. Research in Mathematics Education, 9(1), 3-20. https://doi.org/10.1080/14794800008520167
Goldsmith, L. T., & Seago, N. (2011). Using classroom artifacts to focus teachers’ noticing. In M. G. Sherin, V. R. Jacobs, & R. A. Philipp (Eds.), Mathematics teacher noticing: Seeing through teachers’ eyes (pp. 169-187). Routledge.
Jacobs, V. R., & Spangler, D. A. (2017). Research on core practices in K-12 mathematics teaching. Compendium for research in mathematics education, 766-792.
Josefsson, M. (2013). Characterizations of trapezoids. Forum Geometricorum, 13, 23-35.
Leinhardt, G., & Greeno, J. G. (1986). The cognitive skill of teaching. Journal of Educational Psychology, 78(2), 75-95. https://doi.org/10.1037/0022-0663.78.2.75
Leton, S. I., Djong, K. D., Uskono, I. V., Dosinaeng, W. B. N., & Lakapu, M. (2020). Profile of elementary school teacher in concept understanding of geometry. Infinity Journal, 9(2), 133-146. https://doi.org/10.22460/infinity.v9i2.p133-146
Lewis-Beck, M. S., Bryman, A. E., & Liao, T. F. (2003). The Sage encyclopedia of social science research methods. Sage Publications.
Maher, N., Muir, T., & Chick, H. (2022). Analysing senior secondary mathematics teaching using the Knowledge Quartet. Educational Studies in Mathematics, 110(2), 233-249. https://doi.org/10.1007/s10649-021-10125-1
Mason, J. (2002). Researching your own practice: The discipline of noticing. Routledge.
Mishra, L. (2020). Conception and misconception in teaching arithmetic at primary level. Journal of Critical Reviews, 7(5), 936-939.
Muhtarom, M., Juniati, D., & Siswono, T. Y. E. (2019). Examining prospective teacher beliefs and pedagogical content knowledge towards teaching practice in mathematics class: A case study. Journal on Mathematics Education, 10(2), 185-202. https://doi.org/10.22342/jme.10.2.7326.185-202
Muir, T., Wells, J., & Chick, H. (2017). Developing an understanding of what constitutes mathematics teacher educator PCK : A case study of a collaboration between two teacher educators. Australian Journal of Teacher Education, 42(12), 60-79. https://doi.org/10.14221/ajte.2017v42n12.4
Oates, G., Muir, T., Murphy, C., Reaburn, R., & Maher, N. (2021). What influences mathematics teacher educators’ decisions in course design: Activity theory and professional capital as an investigative approach. In M. Goos & K. Beswick (Eds.), The learning and development of mathematics teacher educators: International perspectives and challenges (pp. 345-366). Springer International Publishing. https://doi.org/10.1007/978-3-030-62408-8_18
Okazaki, M. (2009). Process and means of reinterpreting tacit properties in understanding the inclusion relations between quadrilaterals. In Proceedings of the 33rd Conference of the International Group for the Psychology of Mathematics Education, Thessaloniki, Greece.
Paine, L. W., Fang, Y., & Jiang, H. (2015). Reviving teacher learning: Chinese mathematics teacher professional development in the context of educational reform. The first sourcebook on Asian research in mathematics education: China, Korea, Singapore, Japan, Malaysia, and India, 617-638.
Pascual, M. I., Montes, M., & Contreras, L. C. (2021). The Pedagogical Knowledge Deployed by a Primary Mathematics Teacher Educator in Teaching Symmetry. Mathematics, 9(11), 1241. https://doi.org/10.3390/math9111241
Rowland, T. (2013). The knowledge quartet: The genesis and application of a framework for analysing mathematics teaching and deepening teachers’ mathematics knowledge. Sisyphus—Journal of Education, 1(3), 15-43.
Shulman, L. S. (1986). Those who understand: Knowledge growth in teaching. Educational researcher, 15(2), 4-14. https://doi.org/10.3102/0013189X015002004
Simpson, A., & Haltiwanger, L. (2017). “This is the First Time I’ve Done This”: Exploring secondary prospective mathematics teachers’ noticing of students’ mathematical thinking. Journal of Mathematics Teacher Education, 20(4), 335-355. https://doi.org/10.1007/s10857-016-9352-0
Siswono, T. Y. E., Kohar, A. W., Kurniasari, I., & Hartono, S. (2017). Inconsistency among beliefs, knowledge, and teaching practice in mathematical problem solving: A case study of a primary teacher. Southeast Asian Mathematics Education Journal, 7(2), 27-40. https://doi.org/10.46517/seamej.v7i2.51
Spangenberg, E. D. (2021). Manifesting of pedagogical content knowledge on trigonometry in teachers' practice. Journal of Pedagogical Research, 5(3), 135-163. https://doi.org/10.33902/JPR.2021371325
Star, J. R., & Strickland, S. K. (2008). Learning to observe: using video to improve preservice mathematics teachers’ ability to notice. Journal of Mathematics Teacher Education, 11(2), 107-125. https://doi.org/10.1007/s10857-007-9063-7
Turnuklu, E. B., & Yesildere, S. (2007). The pedagogical content knowledge in mathematics: pre-service primary mathematics teachers' perspectives in Turkey. Issues in the Undergraduate Mathematics Preparation of School Teachers, 1, 1-13.
Usiskin, Z. (2008). The classification of quadrilaterals: A study in definition. Information Age Publishing, Inc.
Wu, Y., & Cai, J. (2016). Progression and implications of research on mathematics teacher educator. Studies in Foreign Education, 43(5), 3-16.
Wu, Y., & Cai, J. (2021). Supporting secondary mathematics teacher educators in China: Challenges and opportunities. In M. Goos & K. Beswick (Eds.), The learning and development of mathematics teacher educators: International perspectives and challenges (pp. 321-341). Springer International Publishing. https://doi.org/10.1007/978-3-030-62408-8_17
Yin, R. K. (2017). Case study research and applications: Design and methods. Sage.
Yunianto, W., Prahmana, R. C. I., & Crisan, C. (2021). Indonesian mathematics teachers' knowledge of content of area and perimeter of rectangle. Journal on Mathematics Education, 12(2), 223-238. https://doi.org/10.22342/jme.12.2.13537.223-238
Zaslavsky, O., & Leikin, R. (2004). Professional development of mathematics teacher educators: Growth through practice. Journal of Mathematics Teacher Education, 7(1), 5-32. https://doi.org/10.1023/B:JMTE.0000009971.13834.e1
Zopf, D. A. (2010). Mathematical knowledge for teaching teachers: The mathematical work of and knowledge entailed by teacher education. University of Michigan.