Alternative conceptions about proportional reasoning in high school students
##plugins.themes.bootstrap3.article.main##
Abstract
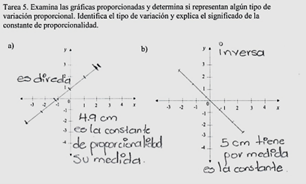
This study aimed to identify alternative conceptions about proportional reasoning among High School Students at a public school located in the state of Guerrero, Mexico. Using a qualitative approach, data were collected through task-based interviews with fifteen students 12th-grade students. Data were analyzed using the thematic analysis method. The findings allowed to identify five alternative conceptions: (1) the variational behavior of a line graph indicates the type of proportional variation; (2) the constant function algebraically represents a proportional variation; (3) a negative slope in the equation of a line indicates an inverse proportional variation; (4) direct proportional variation is conceived as an object; and (5) the constant of proportionality in the graph of a direct proportional variation is interpreted as the length of the line. While this study does not incorporate data from teachers, the findings indicate that instructional strategies prioritizing procedural techniques rather than conceptual understanding. Additional research is required to investigate how teachers' knowledge and instructional methods influence students' development of proportional reasoning. In the same line, the results highlight the need to design instructional strategies that promote the development of more robust proportional reasoning in the High School level.
##plugins.themes.bootstrap3.article.details##

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.
The author is responsible for acquiring the permission(s) to reproduce any copyrighted figures, tables, data, or text that are being used in the submitted paper. Authors should note that text quotations of more than 250 words from a published or copyrighted work will require grant of permission from the original publisher to reprint. The written permission letter(s) must be submitted together with the manuscript.References
Aragón Ruiz, M. (2023). Propuesta STEM para la enseñanza de la proporcionalidad en ESO mediante el razonamiento y la demostración https://uvadoc.uva.es/handle/10324/73984
Balderas-Robledo, R. G., Block-Sevilla, D., & Guerra-Ramos, M. T. (2014). Sé cómo se hace, pero no por qué": Fortalezas y debilidades de los saberes sobre la proporcionalidad de maestros de secundaria [I know how to do it, but not why: Strengths and weaknesses of secondary school teachers' knowledge of proportionality]. Educación matemática, 26(2), 7–32. https://www.redalyc.org/pdf/405/40532665002.pdf
Ball, D. L., Thames, M. H., & Phelps, G. (2008). Content knowledge for teaching: What makes it special? Journal of Teacher Education, 59(5), 389–407. https://doi.org/10.1177/0022487108324554
Bostan-Sarioglan, A. (2016). Conceptual level of understanding about sound concept: Sample of fifth grade students. e-International Journal of Educational Research, 7(1), 87–97. https://files.eric.ed.gov/fulltext/ED565788.pdf
Braun, V., & Clarke, V. (2012). Thematic analysis. In H. Cooper, P. M. Camic, D. L. Long, A. T. Panter, D. Rindskopf, & K. J. Sher (Eds.), APA handbook of research methods in psychology, Vol. 2. Research designs: Quantitative, qualitative, neuropsychological, and biological (pp. 57–71). American Psychological Association. https://doi.org/10.1037/13620-004
Butto, C. M., Delgado Fernández, J., Calderón Araujo, D., & Bazán Ramírez, A. (2019). El razonamiento proporcional en educación básica [Proportional reasoning in basic education]. Horizontes pedagógicos, 21(2), 39–52. https://doi.org/10.33881/0123-8264.hop.21204
Byerley, C., & Thompson, P. W. (2017). Secondary mathematics teachers’ meanings for measure, slope, and rate of change. The Journal of Mathematical Behavior, 48, 168–193. https://doi.org/10.1016/j.jmathb.2017.09.003
Castro-Fernández, F., Lop-Herrera, R., & Juárez-López, J. (2024). The concept of variable and the 3UV model: A literature review. 5, 21–31. https://doi.org/10.34007/jdm.v5i1.2105
Chhabra, M., & Baveja, B. (2012). Exploring minds: Alternative conceptions in science. Procedia - Social and Behavioral Sciences, 55, 1069–1078. https://doi.org/10.1016/j.sbspro.2012.09.599
Chi, M. T. H., Roscoe, R. D., Slotta, J. D., Roy, M., & Chase, C. C. (2012). Misconceived causal explanations for emergent processes. Cognitive Science, 36(1), 1–61. https://doi.org/10.1111/j.1551-6709.2011.01207.x
Cuevas-Vallejo, A., Islas-Ortiz, E., & Orozco-Santiago, J. (2023). Promover el razonamiento proporcional mediante la tecnología digital. Apertura (Guadalajara, Jal.), 15(1), 84–101. https://doi.org/10.32870/Ap.v15n1.2344
Dávila-Araiza, M., & Herrera Garcia, K. (2021). Reflexiones en torno al diseño de una propuesta formativa sobre variación lineal orientada a futuros profesores de secundaria [Reflections on the design of a training proposal on linear variation for future secondary school teachers]. Sahuarus: Revista Electrónica de Matemáticas, 5(1), 94–111. https://doi.org/10.36788/sah.v5i1.114
Denbel, D. (2014). Students’ misconceptions of the limit concept in a first calculus course. Journal of Education and Practice, 5(34), 24–40. https://core.ac.uk/download/pdf/234636567.pdf
Dolores-Flores, C. (2004). Acerca del análisis de funciones a través de sus gráficas: Concepciones alternativas de estudiantes de bachillerato [About the analysis of functions through their graphs: Alternative conceptions in high school students]. RELIME. Revista latinoamericana de investigación en matemática educativa, 7(3), 195–218. https://www.redalyc.org/pdf/335/33570301.pdf
Duit, R., & Treagust, D. F. (2003). Conceptual change: A powerful framework for improving science teaching and learning. International Journal of Science Education, 25(6), 671–688. https://doi.org/10.1080/09500690305016
Fernández-Verdú, C., & Llinares-Ciscar, S. (2012). Características del desarrollo del razonamiento proporcional en la educación primaria y secundaria [Characteristics of the development of proportional reasoning in primary and secondary education]. Ensenanza De Las Ciencias, 30(1), 129–142. https://doi.org/10.5565/rev/ec/v30n1.596
García-García, J. (2018). Conexiones matemáticas y concepciones alternativas asociadas a la derivada y a la integral en estudiantes del preuniversitario Doctoral dissertation. Universidad Autónoma de Guerrero].
Goldin, G. A. (2012). A scientific perspective on structured, task-based interviews in mathematics education research. In A. E. Kelly & R. A. Lesh (Eds.), Handbook of research design in mathematics and science education (pp. 517–545). Routledge.
Hernández-Solís, L. A., Batanero, C., & Gea, M. M. (2024). Relación entre la construcción de espacios muestrales y el razonamiento proporcional de estudiantes costarricenses [Relationship between the construction of sample spaces and the proportional reasoning of Costa Rican students]. Revista de Educación Estadística, 3, 1–28. https://doi.org/10.29035/redes.3.1.1
Hill, H. C. (2007). Mathematical knowledge of middle school teachers: Implications for the no child left behind policy initiative. Educational Evaluation and Policy Analysis, 29(2), 95–114. https://doi.org/10.3102/0162373707301711
Hill, H. C., Ball, D. L., & Schilling, S. G. (2008). Unpacking pedagogical content knowledge: Conceptualizing and measuring teachers' topic-specific knowledge of students. Journal for Research in Mathematics Education JRME, 39(4), 372–400. https://doi.org/10.5951/jresematheduc.39.4.0372
Kaplan, A., Ozturk, M., & Ocal, M. F. (2015). Relieving of misconceptions of derivative concept with derive. International Journal of Research in Education and Science, 1(1), 64–74.
Karplus, R., Pulos, S., & Stage, E. K. (1983). Early adolescents' proportional reasoning on ‘rate’ problems. Educational Studies in Mathematics, 14(3), 219–233. https://doi.org/10.1007/BF00410539
Kastberg, S. E. (2002). Understanding mathematical concepts: The case of the logarithmic function Doctoral dissertation. University of Georgia]. https://jwilson.coe.uga.edu/Pers/Dissertations/kastberg_signe_e_200205_phd.pdf
Lamon, S. J. (2007). Rational numbers and proportional reasoning: Toward a theoretical framework for research. In F. Lester (Ed.), Second handbook of research on mathematics teaching and learning (Vol. 1, pp. 629–668).
Lamon, S. J. (2012). Teaching fractions and ratios for understanding: Essential content knowledge and instructional strategies for teachers. Routledge. https://doi.org/10.4324/9780203803165
Lobato, J., Orrill, C., Druken, B., & Jacobson, E. (2011). Middle school teachers’ knowledge of proportional reasoning for teaching. In Annual Meeting of the American Educational Research Association (AERA).
Lugo-Lugo, C. A., García-Torres, E., & Palmas-Pérez, S. A. (2023). El razonamiento proporcional de alumnos de telesecundaria unitaria a través del uso de micromundos [Proportional reasoning of students in single-tele-secondary schools through the use of microworlds]. In E. L. Juárez Ruiz, L. A. Hernández Rebollar, & A. Castañeda (Eds.), Tendencias en la Educación Matemática 2023 (pp. 135–156). SOMIDEM Editorial. https://doi.org/10.24844/SOMIDEM/S3/2023/01-07
Luque-Álvarez, K. P., & Ibarra-Olmos, S. E. (2021). El papel de las pruebas escritas en la evaluación de los aprendizajes sobre el tema de proporcionalidad [The role of written tests in the assessment of learning on the topic of proportionality]. SAHUARUS: Revista Electrónica De Matemáticas., 5(1), 64–80.
Luque-Álvarez, K. P., & Ibarra-Olmos, S. E. (2021). Significados de la proporcionalidad promovidos por profesores mexicanos en segundo grado de la escuela secundaria [Meanings of proportionality promoted by Mexican teachers in the second grade of secondary school]. Revista Chilena de Educación Matemática, 13(2), 56–67. https://doi.org/10.46219/rechiem.v13i2.52
Mochón-Cohen, S. (2012). Enseñanza del razonamiento proporcional y alternativas para el manejo de la regla de tres [Teaching proportional reasoning and alternatives to the rule of three]. Educación matemática, 24(1), 133–157. https://doi.org/10.24844/EM2401.05
Moreno-León, R. (2023). El pensamiento proporcional y la formación de subjetividades en el aula: Una aproximación al estado del arte [Proportional thinking and the formation of subjectivities in the classroom: An approach to the state of the art]. Revista Venezolana de Investigación en Educación Matemática, 3(3), 1–21. https://doi.org/10.54541/reviem.v3i3.68
Moss, J., & McNab, S. L. (2011). An approach to geometric and numeric patterning that fosters second grade students’ reasoning and generalizing about functions and co-variation. In J. Cai & E. Knuth (Eds.), Early algebraization: A global dialogue from multiple perspectives (pp. 277–301). Springer. https://doi.org/10.1007/978-3-642-17735-4_16
Ramírez, C. J., & Hernández, H. (2017). Dificultades de la noción de la proporcionalidad en el tránsito del nivel primario al secundario [Difficulties of the notion of proportionality in the transition from primary to secondary level]. Revista pakbal(39), 12–18. https://core.ac.uk/download/pdf/33251237.pdf
Ramírez, M., & Block Sevilla, D. (2009). La razón y la fracción: un vínculo difícil en las matemáticas escolares [The fraction and the ratio: A difficult link in school mathematics]. Educación matemática, 21(1), 63–90. https://www.redalyc.org/articulo.oa?id=40516761004
Reyes-Gasperini, D. (2016). Empoderamiento docente y Socioepistemología. Un estudio sobre la transformación educativa en Matemáticas [Teacher empowerment and socio-epistemology: A study on educational transformation in mathematics]. Gedisa.
Rivas, M. A., Godino, J. D., & Castro, W. F. (2012). Development of knowledge for teaching proportionality in prospective elementary teachers. Bolema: Boletim de Educação Matemática, 26(42), 559–588. https://doi.org/10.1590/S0103-636X2012000200008
Salgado-Beltrán, G. (2020). Conceptualizaciones de pendiente que poseen los profesores del bachillerato y las que enseñan a sus estudiantes Doctoral disertation. Universidad Autónoma de Guerrero]. http://ri.uagro.mx/bitstream/handle/uagro/3834/TD_5142653_20.pdf
Salgado-Beltrán, G., & García-García, J. (2024). Conexiones Matemáticas utilizadas por profesores mexicanos de nivel medio superior al resolver tareas sobre la pendiente [Mathematical connections used by Mexican upper secondary teachers when solving tasks on slope]. PNA. Revista de Investigación en Didáctica de la Matemática, 18(3), 255–283. https://doi.org/10.30827/pna.v18i3.27691
Secretaría de Educación Pública. (2023). La Nueva Escuela Mexicana [The new Mexican school]. Secretaría de Educación Pública.
Serhan, D. (2015). Students' understanding of the definite integral concept. International Journal of Research in Education and Science, 1(1), 84–88. https://files.eric.ed.gov/fulltext/EJ1105099.pdf
Soto-Quiñones, M., Rendon, L. M., & Daniel, O. (2024). La proporcionalidad en la formación de profesores. Del programa cognitivo al programa epistemológico [Proportionality in teacher training: From the cognitive program to the epistemological program]. Revista De Investigación Educativa, Intervención Pedagógica Y Docencia, 2(1), 90–107. https://doi.org/10.71770/rieipd.v2i1.2305
Weiland, T., Nagar, G. G., Orrill, C. H., & Burke, J. (2015). Analyzing coherence of teachers’ knowledge relating fractions and ratios. In Proceedings of the 37th annual meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, (pp. 980–983).
Weiland, T., Orrill, C. H., Nagar, G. G., Brown, R. E., & Burke, J. (2021). Framing a robust understanding of proportional reasoning for teachers. Journal of Mathematics Teacher Education, 24(2), 179–202. https://doi.org/10.1007/s10857-019-09453-0